Space is big, but just how large are the star systems in 8-bit Elite?
Unlike its sequels, the original version of Elite doesn't claim to be a space simulator; instead it's a space game, with space-game physics and a space-game flight model in a procedurally generated space-game universe. And it's a great space game, too, possibly even the greatest.
But the in-game feeling of actually being in space is genuinely convincing, and the lore-heavy manual is crammed with so many facts and figures that it's easy to think of the Elite universe as a real place; immersion, after all, is one of Elite's magic ingredients.
As someone who fondly remembers that feeling of the Elite universe being real, I have some questions. Just how big is the Elite universe? And how large are the ships and suns and planets that populate this virtual space? And just how destructive is that crazy energy bomb?
This article is an attempt to discover the scale of 8-bit Elite by looking at the code. Because this is a game and not an accurate simulation, there will be lots of contradictions and incorrect scaling along the way... but the journey is an interesting one, so let's see what clues we can find.
How big are the ships?
----------------------
Ship wireframes are stored as sets of vertices, edges and faces - see the deep dive on ship blueprints for details. The vertices are the points that make up each wireframe, and they consist of sign-magnitude 3D coordinates (x, y, z), with each axis in the range -255 to +255, stored as a one-byte magnitude with a separate sign bit. There is no distinction made between +0 and -0, so each ship design fits inside a bounding box with an edge length of 510 coordinates.
The ship dimensions table in the deep dive on comparing ship specifications is a great way to explore the relative dimensions of the ships in Elite, as you can sort all the blueprints by their individual dimensions. Let's examine a couple of examples here.
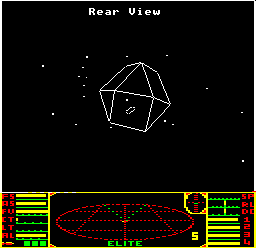
First, consider the Coriolis space station shown above. The vertices in the Coriolis span a range of -160 to +160 along all three axes, giving the station a diameter of 320 coordinates and a shape that sits centrally in the middle of the bounding box.
In comparison, the z-coordinates along the length of the huge Anaconda ship range from -58 at the rear to +254 to the tip of the nose, so the ship points forwards along the z-axis, with the nose almost touching the edge of the bounding box. This gives the Anaconda a length of 312 coordinates, which is a pretty tight fit inside a station that's only eight coordinates wider. Indeed, the Anaconda is more than twice the length of the Cobra Mk III, which is 150 coordinates from nose to tail (including a front laser gun of length 14), with a width of 256 and a height of 50.
It's worth noting that object dimensions can be a bit strange in Elite - the relative sizes of some of the objects within the bubble make little sense. For example, items like the cargo canister (48w x 29h x 30d) and missile (24w x 24h x 112d) are absolutely massive compared to the ships that are supposed to carry them. For example, 20 cargo canisters - which is the standard cargo capacity of a Cobra Mk III - would take up almost the same volume in space as six entire Cobras, so even if the stacking robots in the hold were able to work miracles, this is way off the expected scale.
Similarly, the diameter of a Coriolis station equals just 2.9 missiles laid end to end, which makes absolutely no sense whatsoever; both missiles and canisters are clearly massive in the actual game. But if the wireframes were too small, then we'd never be able to spot them in space, so clearly some of these dimensions are optimised for gameplay over realism, and they should be taken with a very large pinch of salt.
Now let's take a look at the planets and suns.
How big are the planets?
------------------------
The first thing to mention is that the planet dimensions shown in the system data have no impact on how the planet is drawn. In 3D space, all planets have the exact same size, so we should take no notice of the Average Radius figure in the System Data screen:
This number is procedurally generated, as described in the deep dive on generating system data, but it isn't stored anywhere or used for anything, so let's ignore it.
Instead, we need to look at the size of the planet when it is spawned, which is done in the SOLAR routine. The planet is spawned in exactly the same way as ships, i.e. with nosev pointing towards us, out of the screen, and with roofv pointing up and sidev pointing right (see the deep dive on orientation vectors for an explanation of these three vectors). The vectors are initialised in the INWK workspace by the ZINF routine, just as with the ships.
When we launch from a space station, the planet is spawned with a radius of:
K(1 0) = (96 0) = 24,576 coordinates
It is spawned at a distance of:
(z_sign z_hi z_lo) = (1 0 0) = 65,536 coordinates
so this is the distance between the centre of the planet and the centre of the station. This is all set up in the TT110 routine, which calls the SOS1 routine to initialise the planet's data block. (Specifically, the planet is spawned with a radius of one unit vector, as discussed in the next section.)
So the planet has a radius of 24,576 coordinates, which gives it a diameter of:
2 * 24,576 = 49,152 coordinates
As a Coriolis station is 320 coordinates wide, that gives the planet a radius of:
24,576 / 320 = 76.8 Coriolis station diameters
and a diameter of:
49,152 / 320 = 153.6 Coriolis stations
The station is spawned at 65,536 coordinates from the planet's centre, at an altitude of:
65,536 - 24,576 = 40,960 coordinates
above the planet surface. This makes it:
65,536 / 320 = 204.8 Coriolis station diameters
from the centre, or:
40,960 / 320 = 128 Coriolis station diameters
above the planet's surface. This is the same as:
65,536 / 24,576 = 2.67 planet radii
from the centre, or:
40,960 / 24,576 = 1.67 planet radii
above the surface, so the planet's surface is a lot closer to the centre of the planet than it is to the station.
If we put a Coriolis station in orbit around the Earth with the same orbital characteristics, then the Coriolis station would be at a much higher altitude than the International Space Station, which orbits at an average of 417.5km above the surface of the Earth, or just 1.066 times the Earth's average radius of 6371km. Our Coriolis station would be orbiting:
2.67 * 6371 = 16,989km
from the centre, at an altitude of:
1.67 * 6371 = 10,618km
above the surface. This is much higher than the majority of Earth satellites, which operate in low Earth orbit at altitudes of up to 2000km, and it's about halfway to the GPS satellite cluster at an orbit of around 20,000km.
How big is the unit vector?
---------------------------
Planet spawning gives us a way to understand the scale of the orientation vectors, which are a core aspect of way Elite works. As discussed in the deep dive on orientation vectors, unit vectors in Elite use a value of (96 0) to represent the unit length of 1.0 (where the low byte is effectively a fractional part). Vectors are normalised to this length in the TIS2 routine, which is used to divide vector coordinates by their length, and TIS2 is called from the NORM routine when normalising vectors (see the deep dive on tidying orthonormal vectors for more details).
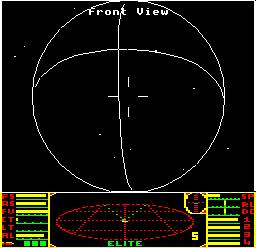
As mentioned above, when we launch from a space station, the planet is spawned with a radius of (96 0) and at a distance of (1 0 0), so the planet's radius is exactly one unit vector. The planet then gets projected onto the screen and drawn by the PLANET routine. As part of this projection, the planet's dimensions get divided by the distance in the z-coordinate, so to get the on-screen radius of the projected planet, we calculate this:
256 * radius / z = 256 * (96 0) / (1 0 0) = (96 0 0) / (1 0 0) = 96
which gives us an on-screen circle with a radius of 96 pixels. The space view is 192 pixels high and 256 pixels wide, so this means that on launching, the planet should exactly fit the space view vertically, as 96 * 2 = 192. This is indeed the case, if you look at the size of the planet on launching in the above screenshot.
How big is the sun?
-------------------
Interestingly, the sun is spawned with exactly the same dimensions as the planet, so we also have a star that's 153.6 space stations in diameter. This is extremely small for a star, especially one that seems to burn quite normally, flickering red and yellow just like our own Sun.
So how far away from the planet is the sun spawned? This is determined using procedural generation, based on the system's seeds (see the deep dive on galaxy and system seeds for more details). The details are in the SOLAR routine: bits 0-2 of seed s1_hi are extracted, bits 0 and 7 are set, and the result is used as z_sign in the sun's 24-bit z-coordinate (z_sign z_hi z_lo).
This means that the sun is always spawned behind us when we arrive in a new system from hyperspace, as the sign bit in bit 7 of z_sign is set, making the sign-magnitude number negative. And it is spawned at a distance of between (1 0 0) and (7 0 0), which ranges from:
(1 0 0) / (96 0) = 65,536 / 24,576
= 2.67 planet radii
to:
(7 0 0) / (96 0) = 458,752 / 24,576
= 18.67 planet radii
The Earth, meanwhile, is an average of 23,455 Earth radii from the Sun, which is a factor of between:
23,455 / 18.67 = 1256 times
and:
23,455 / 2.67 = 8796 times
larger than the distance in Elite, so the tiny stars in Elite are much, much closer to their solitary planets than the Sun is to the Earth. As Father Ted said, "These are small, but the ones out there are far away..."
How fast can we fly?
--------------------
Our current ship speed is stored as a scalar value in the DELTA variable that gets subtracted from the z-coordinates of all other ships in the bubble, thus effectively moving our ship forwards by pushing everything else back. This is done once on each iteration of the main game loop, so speed is effectively measured in coordinates per iteration. Here's the code in part 6 of the MVEIT routine.
The Cobra Mk III we are flying can travel at a top speed of 40. This means we can cover 40 coordinates in one iteration of the main game loop, so at top speed, we can traverse the 320-coordinate length of a Coriolis space station in:
320 / 40 = 8 iterations
The fastest ship in the game is the missile, which travels at a speed of 44, so a missile will always reach its target, given enough time and luck. In joint second place, along with the Cobra Mk III, are the Asp Mk II and the Cougar (shown above), while the Shuttle and escape pod take last place at a speed of just eight coordinates per iteration.
Unfortunately it's a bit hard to translate this into a traditional time-based velocity, as the real-world speed of the main game loop varies depending on how much the computer has to do. As a result, scenes with lots of ships and explosions will slow down very noticeably, while flying through empty space is a relatively quick affair, especially if you switch to a text view to reduce the strain on the graphics routines.
How big is the local bubble?
----------------------------
When we fly around in Elite, we are surrounded by a local bubble of space, with our ship at the very centre (see the deep dive on the local bubble of universe for more details). So how big is this bubble?
Well, the FAROF routine removes ships when they reach a distance of more than:
(224 0) = 57,344 coordinates
away from our ship. So the bubble is actually a sphere of radius 57,344 coordinates, which is the same as:
57,344 / 320 = 179.2 Coriolis station diameters
or:
57,344 / 24,576 = 2.34 planet radii
So it's a pretty large playing area.
This also means that the energy bomb, which blows up everything within the local bubble, has a blast radius of:
57,344 / 49,152 = 1.17 planet diameters
So our humble Cobra Mk III can house an energy bomb, that we can buy for just 900 credits, that is capable of destroying an entire planet and pretty much everything in low-to-medium orbit around it. Ouch!
The system we are flying through is a lot bigger than our local bubble, so let's look at that next.
How far is the in-system jump?
------------------------------
When flying through space, the planet and sun gradually move relative to us. Because our ship is always at the centre of the Elite universe, they actually move in the opposite direction to our flight path while our ship stays at the origin. When we press "J" to do an in-system jump, they do the exact same thing, but we jump a noticeable distance in one go. So how far do we jump?
The WARP routine implements the in-system jump. Just like standard propulsion, we don't actually move at all - instead, the planet and sun move backwards, in the opposite direction to where we're travelling. This makes it feel as if we are jumping through space, when in reality the planetary system is the one doing the jumping (this is also why space junk comes along for the ride when we jump, as it stays with us in our stationary local bubble).
The WARP routine starts by checking that we are able to do an in-system jump, making sure there are no other ships around, we aren't in witchspace, and that we aren't about to jump too close to the planet or sun. Assuming all is well, WARP decrements the top byte of the 24-bit coordinates for the sun and planet, like this:
(z_sign z_hi z_lo) = (z_sign z_hi z_lo) - (1 0 0)
So the distance we move during each in-system jump is the same as the distance between the space station and the centre of the planet, which is:
(1 0 0) = 65,536 coordinates
or:
65,536 / 320 = 204.8 Coriolis station diameters
or:
65,536 / 24,576 = 2.67 planet radii
And how does this in-system jump compare to the size of the whole star system? Let's take a look...
How big is each star system?
----------------------------
There isn't really a "star system" in Elite as such. There is only our local bubble, containing our ship at the centre and possibly some other nearby ships; and then there are the planet and the sun (or station, as we can only have one of the station or sun spawned at any one time).
But the bubble is separate to the planet and sun, and we can fly away from them - a long way away from them, it turns out. The size of the coordinate system is 24 bits, with coordinates being stored as numbers of the form (z_sign z_hi z_lo). These are sign-magnitude numbers, with the top bit storing the sign, so that gives us a coordinate range of +/- 23 bits, or -8,388,607 to +8,388,607. These coordinates are the same as the ones used in the ship wireframes and planet spawning, so each system is a cube of:
2 * 8,388,607 = 16,777,214 coordinates
in size (as no distinction is made between +0 and -0), so that's:
16,777,214 / 320 = 52,429 Coriolis station diameters
or:
16,777,214 / 49,152 = 341.3 planet diameters
This is pretty big, but it is still finite. So can we fall off the edge of space? Let's see...
Can we jump beyond the edge of space?
-------------------------------------
As noted above, when we do an in-system jump, the sun and the planet are moved relative to us, so the local bubble stays at the origin, but the sun and planet jump away from us in the opposite direction to travel. So what happens if we keep jumping until we reach the edge of the star system?
The in-system jump routine at WARP calls the ADD routine to move the sun and planet backwards, The call to ADD subtracts 1 from the top byte of the z-coordinates of the planet and sun, which is the same as subtracting (1 0 0) from (z_sign z_hi z_lo). This calculation moves the planet and sun backwards by (1 0 0) coordinates, or 65,536, on each jump.
So if we start close by to the planet, at z-coordinate (0 z_hi z_lo), and jump away using in-system jumps, then, in theory, 127 in-system jumps would push the planet and sun backwards, right to the edge of the coordinate system, in the vicinity of z-coordinate -(127 z_hi z_lo). Given that nearby ships prevent in-system jumps, we would have to be pretty determined to get this far - but it is possible.
The ADD routine doesn't check for overflows, so if the planet or sun go past the edge of the coordinate system, then the top bytes of their z-coordinates will simply wrap around to zero, while keeping the same sign (they don't wrap around to the opposite end of the star system, as the coordinates are sign-magnitude numbers, not signed two's complement numbers).
So say the planet is now behind us at z-coordinate -(127 z_hi z_lo) and we do in-system jump number 128, then the top byte of the planet's new z-coordinate will be calculated as follows:
- Take the top byte, which is -127, or %11111111
- Remove the sign bit of the top byte to give 127, or %01111111
- Add 1 to give 128, or %10000000
- Apply the correct sign bit for the result, to give %10000000
- So the result is -(0 z_hi z_lo)
This means the planet will suddenly appear out of nowhere and only slightly behind us, effectively jumping forward from the most distant reaches of the star system and right into our ship's z-plane. Though because the only way this can happen is if the planet is behind us and we are jumping away from it, we won't see it suddenly appear close behind us unless we are looking backwards or sideways, or turn around.
So the game doesn't crash if we jump too far, but instead the planet will suddenly appear somewhere behind us. It could, of course, be a long way off to the sides, or way above or below us, in which case we probably won't notice. But if we are unlucky, we can crash: if the values of z_hi and z_lo in the above are very small then the planet will wrap around to a position that's very close behind us, so if the distance to the planet is also small in the x- and y-coordinates, then on the next iteration the altitude detection routines might decide that we are too close to the surface or even inside the planet, and we will die instantly and without any warning.
This calculation also applies to the sun, so there are two ways of crashing into the edge of a star system, though this would still be pretty unlucky as space is very big, even in Elite's finite universe.
And does this apply if we jump almost to the edge of space and then fly the rest of the way? Let's see...
Can we fly beyond the edge of space?
------------------------------------
What if we jump 127 times, almost to the edge of space, and then fly the final few coordinates, right up to the edge of the coordinate system?
Well, it looks like the same maths will apply. Our speed delta gets applied to the z-coordinates of the planet, sun and other ships in the vicinity by part 6 of MVEIT, which calls the MVT1 routine to do the addition.
As with the ADD routine used by the jump calculation, MVT1 doesn't check for overflow, so if the result overflows the 24-bit sign-magnitude coordinate, it will jump back to a little over zero, just as before. So if we are flying away from the planet and the planet reaches the edge of the star system behind us, then the planet will suddenly appear around z-coordinate 0. As with the in-system jump, if the planet's x- and y-coordinates are large enough then this means it will appear somewhere to the side or above or below, but if they aren't very large then we could easily find ourselves inside the planet, and we'll die instantly. And, of course, it's the same for the sun.
Given how tight memory is in Elite, I guess the authors figured that checking for overflow wasn't worth the extra bytes. I wonder if anyone ever did jump this far in the original game; I suspect people tried, but they probably gave up well before 127 jumps, as that's an awful lot. And even if they did wrap around, they wouldn't necessarily have noticed unless they suddenly died on the spot. Who knows...
How big is the galaxy?
----------------------
Each galaxy contains 256 star systems, so the eight galaxies together give us a total of 2000 different systems to explore. The Long-range Chart shows just how big each galaxy is:
The circle in the bottom-left corner shows our current jump range, which in this example is 7.0 light years. But how big is the galaxy itself?
The chart is drawn by the TT22 routine. In the original BBC Micro version, the chart is 128 pixels tall and 256 pixels wide, and the screen coordinate of each system is given by the s1_hi seed for the x-coordinate (which is in the range 0 to 255), and the s0_hi seed shifted right by one place for the y-coordinate (which is in the range 0 to 127); see the deep dive on galaxy and system seeds for more details.
So what does this 256x128-pixel chart represent in terms of light years? Well, TT22 calls the TT14 routine to draw the fuel circle, which is the clue we need. This routine calculates the radius of the fuel circle by taking the current fuel level from the QQ14 variable and right-shifting it by two places, which divides it by 4 and rounds it down to the nearest integer. The result is the fuel circle's radius in pixels.
The fuel level is stored as the number of light years * 10, so when we have a full fuel tank of 7.0 light years, QQ14 contains 70. The pixel radius of the fuel circle for a full tank is therefore:
70 >> 2 = 17 pixels
So 7.0 light years in the Long-range Chart equals 17 pixels, which means each pixel represents:
7.0 / 17 = 0.41 light years
So the whole chart shows a galaxy that's:
256 * 0.41 = 105.4 light years
wide, and:
128 * 0.41 = 52.7 light years
high.
If we spaced out the 256 systems equally in a grid throughout this area of space, then there would be an average of 22.6 systems across the width of the map and 11.3 systems along the height, as:
22.6 * 11.3 ~= 256
So the average gap between each system would be:
105.4 / 22.6 = 4.65 light years
which is pretty close to the distance from the Earth to our nearest star, Proxima Centauri, at a distance of 4.25 light years.
So the galaxies in Elite have a fairly similar star density to our own corner of the Milky Way, though they are an awful lot smaller than our home: the Milky Way is around 87,400 light years across, which is 853 times wider than the 105.4 light years of the Elite galaxies.
Converting to a human scale
---------------------------
All the dimensions I've talked about so far have been in 3D space coordinates, which we can convert into Coriolis station diameters, planet radii and so on. We can compare some of these relative dimensions to the equivalents on Earth, such as "the station orbits at an altitude of 1.67 planet radii", but how do Elite's coordinates map onto the units of measurement in the real, human world?
Not particularly well, it turns out. There are some clues in the Space Trader's Flight Training Manual that we can use to estimate just how big things are in Elite, but they produce contradictory and nonsensical results, which is perhaps not that surprising as the manual doesn't claim to be that accurate. Still, let's give it a go.
The Space Trader's Flight Training Manual has a big clue on page 16:
Each Coriolis station has a diameter of 1 standard kilometre. They can berth 2000 ships, and support a fair-sized colonial life development of humanoids.
Given that the Coriolis is 320 space coordinates wide, this means that 320 coordinates is 1km, so each coordinate is:
1km / 320 = 1000m / 320
= 3.125 metres
Then there are the ship dimensions in the back of the book, in the section titled Jane's Galactic Ships and Remote Colonial Construction, 5th Edition, 3205 (pub. Trantor House). Here we can see that the Cobra Mk III, for example, is 130ft wide. 130ft is 39.6 metres, and the width of the Cobra wireframe is 256 coordinates, so this makes each coordinate:
39.6m / 256 = 0.155 metres
which is a factor of 20 smaller than our first estimate.
And on page 33, we learn that the energy bomb has a "heat radius" of 9000km. Given that it clears the local bubble of all known life, and the local bubble has a radius of 57,344 coordinates, that gives us a coordinate size of:
9000km / 57,344 = 9,000,000m / 57,344
= 156.9 metres
which is a factor of 50 larger than our first estimate.
Of course, for the latter scenario, all we know from the game code is that the energy bomb destroys everything within the bubble, but in lore terms it could be destroying plenty that's outside the bubble as well - the game just doesn't happen to model anything beyond the edge of the bubble, so we wouldn't know. And in "real life", ships wouldn't magically appear from nowhere at the bubble's edge like they do in the game, so maybe the bubble is actually the range of the ship's sensors, in which case it wouldn't be related to the size of the energy bomb blast at all? It's difficult to know.
We can't even turn to the concept of the astronomical unit, which is the average distance between our Sun and the Earth. Is there an astronomical unit in Elite? Not really; as we saw above, the distance between each star and its accompanying planet varies from 2.67 to 18.67 planet radii. So not only is there no constant astronomical unit between the different star systems, but the measurements aren't even in the same ballpark as our own solar system. The average distance between the Earth and Sun - i.e. 1 astronomical unit - is 23,455 Earth radii. This is between 1256 and 8796 times larger than the planet-sun distance in Elite, so that doesn't work at all.
So the real world measurements from the manual are wildly incompatible with each other, and there isn't enough consistency to tie the Elite star systems to our own solar system's astronomical unit. But let's arbitrarily choose the 1km size of a Coriolis station as the correct scale, and plug this figure into the results anyway, because why not...
A summary
---------
Here's a summary of all the coordinate-relative sizes in the above, along with their equivalent distances in kilometres if we assume a Coriolis station has a diameter of 1km.
| Measurement | Coordinates | If Coriolis = 1km |
|---|---|---|
| Cobra Mk III top speed | 40 per iteration | 0.125km per iteration |
| Cargo canister length | 48 | 0.15km |
| Missile length | 112 | 0.35km |
| Cobra Mk III width | 256 | 0.8km |
| Coriolis station width | 320 | 1.0km |
| Planet radius | 24,576 | 76.8km |
| Planet diameter | 49,152 | 153.6km |
| Station distance from planet centre | 65,536 | 204.8km |
| Station altitude above surface | 16,384 | 51.2km |
| Sun radius | 24,576 | 76.8km |
| Sun diameter | 49,152 | 153.6km |
| Local bubble radius | 57,344 | 179.2km |
| Local bubble diameter | 114,688 | 358.4km |
| In-system jump | 65,536 | 204.8km |
| Star system cube size | 16,777,214 | 52,428.8km |
This is all in a galaxy that's 105.4 light years wide and 52.7 light years across.
Some of the kilometre figures are massively unrealistic. For a start, a sun with a diameter of 153.6km would be a small white dwarf tottering on the brink of becoming a neutron star, which would easily consume everything within a star system of 52,429km in size, particularly such tiny asteroid-scale planets as these. And imagine trying to dock an 800m-wide Cobra through a slot in a 1000m-wide station; even a docking computer would struggle with that.
So I think it's safe to say that the flight manual might not be a work of hard science fiction... but the 8-bit Elite universe is still a very real place in the player's mind, and that, of course, is the most important point.