The algorithms behind the huge craters of planets like Diso
There is some debate around planets like Diso and Leesti. As Lave's closest neighbours, with each one an easy 3.6-light-year hop from the starting point, these two systems are most players' first experience of a cratered planet. Leesti, for example, looks like this:
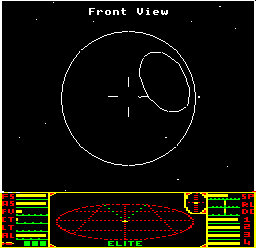
Now, some people believe this circle that races around the planet is a giant storm cloud on a gaseous giant, like Jupiter's famous Red Spot. There isn't enough detail in the game's graphics to dispel this notion, and there are no clues in either the source code, the manual, the novella or Ian Bell's Elite website. But personally, I think this feature is a crater, because Diso is populated by Black Furry Felines enjoying an agricultural economy on a planet with a radius of just 6155km, while Leesti has a human population living on a tiny planet of radius 3085km. Jupiter, in contrast, is over twenty times the size, and even black cats would run out of lives in that kind of atmosphere.
Also, to my eyes, both planets look just like Saturn's moon Mimas that was so memorably photographed by Voyager 1 back in November 1980:



Surely Diso's design was inspired by this epic image, which came out at exactly the right time to influence the game's authors. And everyone who's seen Star Wars and has hyperspaced into Leesti has surely thought at some point, "That's no moon!" After all, Elite was developed during the classic Star Wars run between 1977 and 1983, and there must be an influence there; heck, the 6502 Second Processor version even includes a Star Wars scroll text (see the deep dive on the 6502 Second Processor demo mode for the details).
So, on this site at least, Diso and Leesti have craters rather than giant storms, so that's what we're going to look at here.
Planet types
------------
In the BBC version of Elite, planets come in two types - those with craters (like Diso and Leesti, as shown above) and those with meridians and equators (like Lave, as shown in the deep dive on drawing meridians and equators).
The planet's type depends on its tech level, and it is set in the SOS1 routine that creates the planet's ship data block. Each system has a procedurally generated tech level in the range 0 to 14, which is incremented by the TT25 routine to give a final on-screen tech level in the range 1 to 15 (see the deep dive on generating system data for details). The rule is simple: if bit 1 of the generated tech level (0 to 14) is set then the planet has a crater, otherwise it has a meridian and an equator.
This means that planets with a generated tech level ending in %10 or %11 will have craters, so that's 2, 3, 6, 7, 10, 11 and 14. When shown in the Data on System screen, this means that planets with tech levels 3, 4, 7, 8, 11, 12 and 15 will have craters, while tech levels 1, 2, 5, 6, 9, 10, 13 and 14 will have meridians and equators. In this deep dive, we're going to focus on planets with craters.
Orientation vectors
-------------------
Craters are drawn as complete ellipses on the planet's surface. To understand how these ellipses are calculated, we first need to talk about how planets are stored.
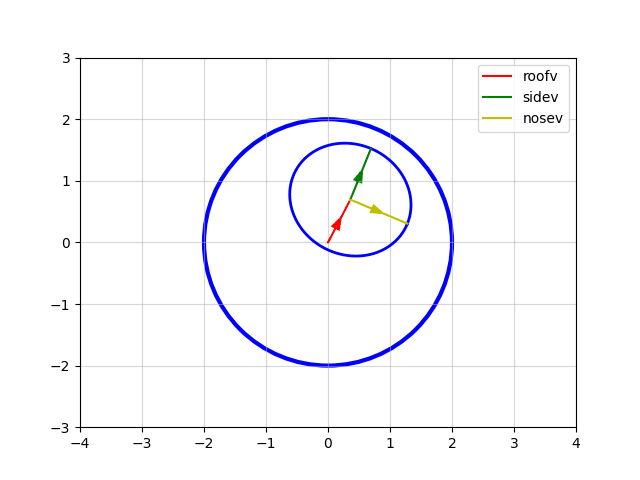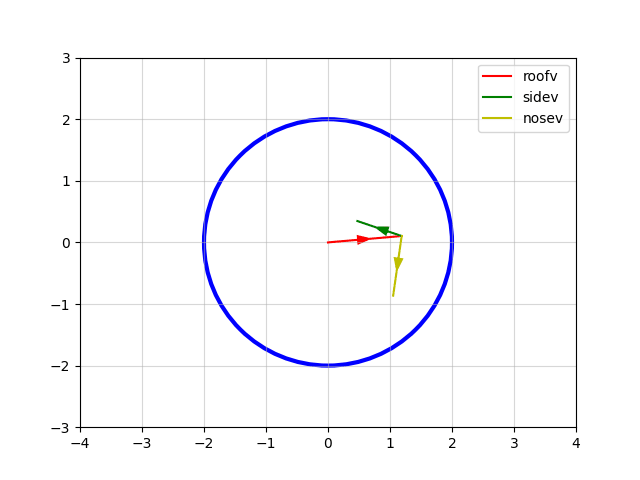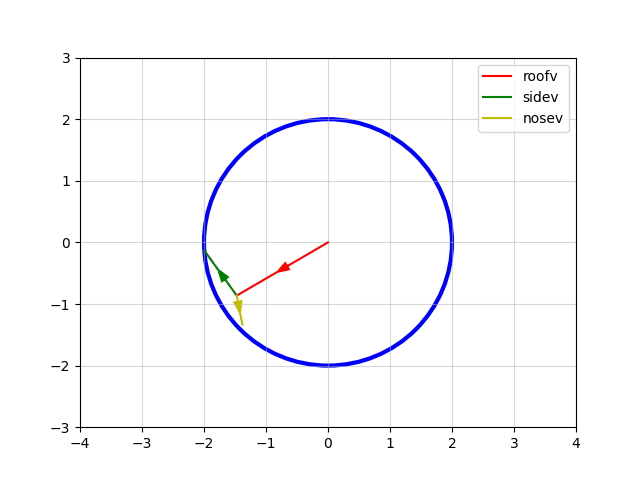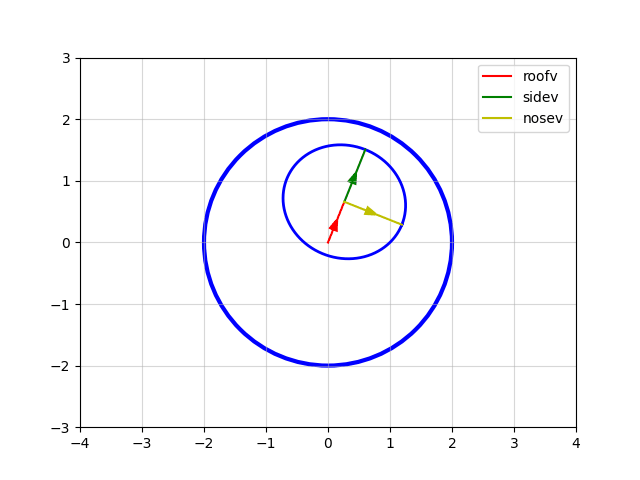
Just like ships, each planet has an orthogonal set of unit vectors - roofv, nosev and sidev - that describe its orientation (see the deep dive on orientation vectors for details). It might seem odd at first why a spherical object such as a planet should need three orthogonal vectors, but they are used to project the circular crater efficiently into the required ellipse, and they also allow the same rotation and 3D projection routines to be used to rotate and display both planets and ships.
Let's see how the orientation vectors are used to calculate the planet's crater.
Calculating the ellipse coordinates
-----------------------------------
The heavy lifting for calculating the crater's ellipse coordinates is done by part 3 of the PL9 routine. This routine calculates the following, and then calls the ellipse routine at PLS22 to do the actual plotting.
We start by calculating the centre of the on-screen ellipse, in pixel coordinates:
x = K3(1 0) = 0.87 * roofv_x + pixel x-coordinate of planet centre
-------
z
y = K4(1 0) = 0.87 * roofv_y - pixel y-coordinate of planet centre
-------
z
In the above, z is the z-coordinate of the planet's centre in 3D space, i.e. how far in front of us the planet is, as the z-axis points into the screen (see the deep dive on pitching and rolling for more on this). The planet's orientation vectors are in roofv, nosev and sidev, and they describe the orientation of the planet (see the deep dive on orientation vectors).
The centre of the ellipse is displaced by a factor of 0.87 of the planet's radius towards the centre of the planet, which is calculated by multiplying by 222 and dividing by 256. This means the crater's ellipse is always drawn just slightly inside the planet's two-dimensional circle outline, so it looks like it is on the planet's surface rather than floating above it.
Note that the pixel y-coordinate is negated in the second calculation above because pixel y-coordinates increase as we move down the screen, while 3D y-coordinates increase as we move up in 3D space, so we need to negate the pixel y-coordinate before we can combine it with the vector y-coordinate.
As described in the deep-dive on drawing ellipses, we define our ellipse using two conjugate radius vectors, u and v. For the crater ellipse we calculate these as follows, starting with the first conjugate radius vector in u:
u = [ XX16 K2 ] = [ nosev_x / 2z ]
[ XX16+1 K2+1 ] [ nosev_y / 2z ]
and then the second conjugate radius vector in v:
v = [ XX16+2 K2+2 ] = [ sidev_x / 2z ]
[ XX16+3 K2+3 ] [ sidev_y / 2z ]
Amazingly, these two simple calculations produce valid u and v vectors that define a realistic-looking elliptical crater on the planet's surface. The division by 2z ensures that the crater's diameter is half that of the planet.
The results of the above calculations in K3, K4, XX16 and K2 are passed as arguments to the PLS22 routine, which draws the ellipse. The argument TGT is set to 64, which tells the ellipse routine to plot a full ellipse with these details.
The end result looks like this:


Further analysis
----------------
The crater ellipse is only drawn when the roofv vector is positive (i.e. when it is pointing away from us). This check is made at the very start of part 3 of the PL9 routine, and when roofv is negative and pointing towards us, the crater code is skipped and the crater is therefore not drawn. The net effect of this logic is that the crater only appears on one side of the planet, as you would expect from a solid planet.
To make the planet rotate forever, we set the pitch and roll counters to 127 in the SOS1 routine. This ensures that the counters don't count down, so the planet rotates on every iteration around the main loop, pitching around the sidev vector and rolling around the nosev vector by the same small angle on each iteration. This rotation is handled by the exact same code that handles pitching and rolling of ships - see the deep dive on pitching and rolling by a fixed angle for details.
The 3D vectors sidev and nosev are projected into the 2D u and v vectors by simply ignoring their z-components (i.e. only sidev_x and sidev_y contribute to the v vector above, and sidev_z is ignored). This projects the crater from a 3D circle into a 2D ellipse; technically it is an orthographic projection onto the plane through the centre of the planet, where z is constant and equal to the z-coordinate of the planet's centre (so this is the plane through the planet's centre that is parallel to the screen). In other words, the variation in z-coordinates between the front and the back of the crater, or between the front and back of the planet, is ignored. But the whole ellipse image is rescaled by a single 1/2z factor, to make the ellipse appear an appropriate size compared to the planet, so we get away with this approximation.
It seems amazingly convenient that the u and v vectors from this projection are sufficient to define a realistic-looking ellipse. Mathematically, you need a centre of an ellipse and three points on the ellipse's circumference to define an ellipse. But here we have a centre and only two points on the ellipse's circumference (marked by u and v). However, given that these are also conjugate radius vectors, there is enough information to uniquely define an ellipse (see the Wikipedia entry on conjugate diameters for details).
There is actually a degree of freedom in the choice of sidev and nosev here - we could rotate them both around the red roofv vector shown in the above animation, and this would change u and v; but would this adversely affect the ellipse that gets drawn? Fortunately, it turns out that it does not make any difference to the final ellipse drawn, as demonstrated here:

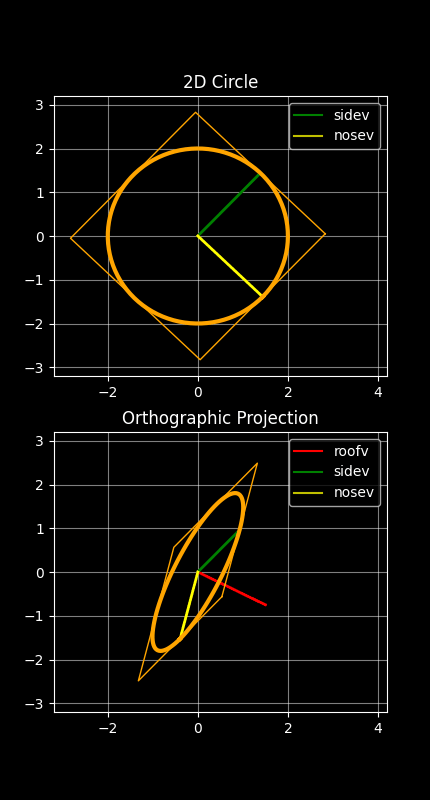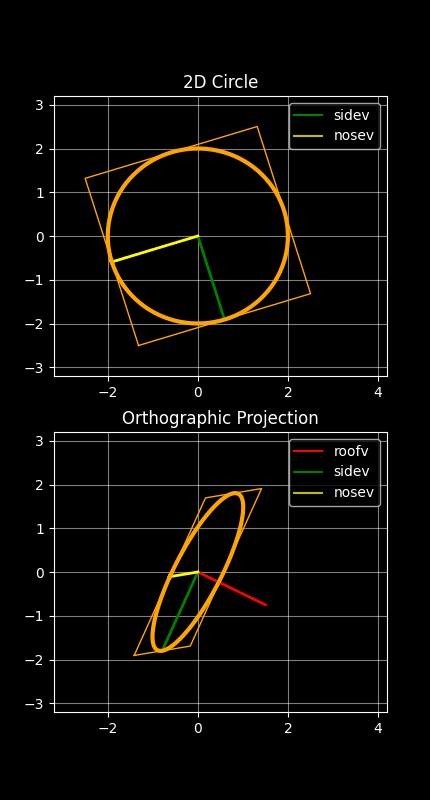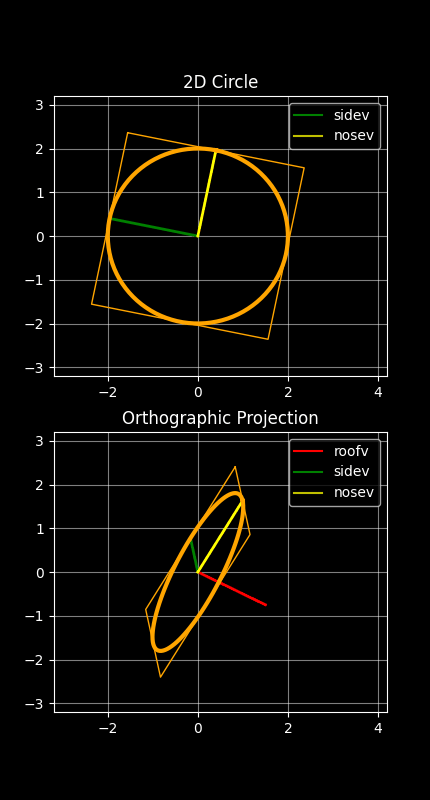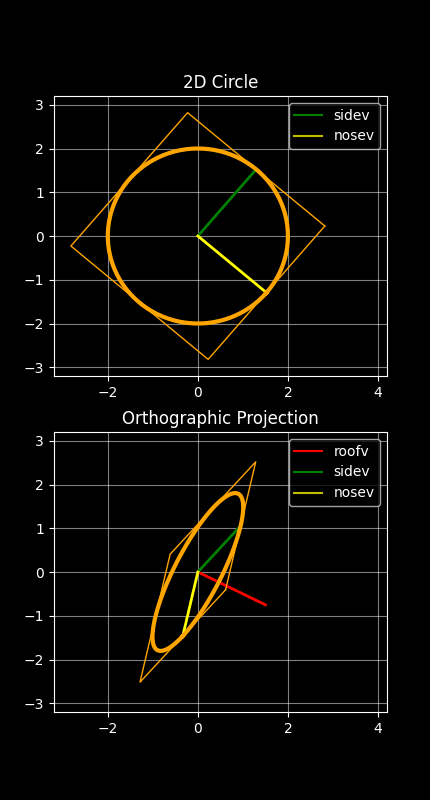

The fact that the ellipse drawn is stable in the animation above - despite it being repeatedly redrawn in each animation frame with the ellipse-drawing algorithm - demonstrates the degree of freedom there is in rotating the green and yellow sidev and nosev vectors about the red roofv vector.
The above animation also shows that the two valid points on the original circle's circumference (u and v) go through an orthographic projection, and so must end up as two valid points on the orthographically projected ellipse. Hence the ellipse required must pass through these two projected points (which it does!). The animation also shows that the bounding square of the original circle becomes a parallelogram in this projection. The parallelogram touches the ends of the u and v vectors, which confirms that those u and v vectors are valid conjugate radii of the ellipse. This means the u and v projections do indeed form two valid conjugate radii of the required ellipse; and hence the ellipse finally drawn is the correct projected ellipse.
All these benefits come from handling the nosev, roofv and sidev vectors for a planet in the same way as we handle them for ships. Along with some clever maths and simplifications in part 3 of the PL9 routine, these benefits - plus the elegant way ellipses are defined in Elite - make the final crater-plotting routine very fast and compact.
A final efficiency of the crater code is that the same STP argument that was used to draw the planet can simply be reused when drawing the ellipse. The STP argument is the angular step rate that we use when plotting a circle or ellipse. The CIRCLE routine intelligently adjusts the STP argument so that planets that are further in the distance, and hence smaller, use a larger STP argument. This means that more distant planets require fewer calculations and fewer lines, resulting in a much faster drawing speed. The calculated STP argument for the planet's circle is reused when drawing the crater ellipse, so that more distant craters are also drawn more quickly.
So that's no moon... but it is a stroke of mathematical genius from the original authors (and in particular Ian Bell, who wrote the planet-plotting and ship-rotation routines discussed above).